機械学習アルゴリズム サポートベクターマシンとPython(scikit-learn編)
執筆者:南波真之
※本記事は吉政創成株式会社「Python学習とキャリアアップ」より寄稿されたコラムとなります。

皆さん、こんにちは。南波真之(なんばさねゆき)と申します。
私はエンジニアではない文系の人間ですが、Pythonの可能性やデータ分析を使った仕事に興味があります。
前回は、分類手法の代表の1つでもあるサポートベクターマシン(SVM)について、基礎編として取り上げてきました。SVMとは機械学習のアルゴリズムで、2つのクラス(データのグループ)の分類を行うことを基本的な目的として利用します。分類のための境界線とそれに最も近い各クラスのデータ(サポートベクター)の間の距離が最も大きくなる(マージンの最大化)ような境界線(決定境界線)を引くということです。
さて今回は、SVMの続きです。SVMをscikit-learnを使って構築してみます。私が勉強しているPythonによるあたらしいデータ分析の教科書(翔泳社)の、P226.〜P.234の部分です。SVMの基礎を理解した上で、Pythonを使ってSVMを作ってみようと思います。
scikit-learnでサポートベクターマシンを使ってプロット
データを用意して、早速サポートベクターマシンを使っていきます。用意するデータは2クラスでランダムに生成したデータを作ります。
np.random.seed(110)
# X軸Y軸ともに0〜1までの分布から100点をサンプリングする
X0 = np.random.uniform(size=(100, 2))
# クラス0のラベルを100個生成
y0 = np.repeat(0, 100)
# X軸Y軸ともに-1〜0までの分布から100点をサンプリングする
X1 = np.random.uniform(-1.0, 0.0, size=(100, 2))
# クラス1のラベルを100個生成
y1 = np.repeat(1, 100)
# プロット figはfigure(図形), axはaxes(軸)
# figureオブジェクトとそれに属する1つのaxesオブジェクトを生成
fig, ax = plt.subplots()
# 散布図 scatter(x座標, y座標, markerマーカースタイル, labelラベル名)
ax.scatter(X0[:, 0], X0[:, 1], marker='o', label='class 0′)
ax.scatter(X1[:, 0], X1[:, 1], marker='x', label='class 1′)
# 軸にラベル付け
ax.set_xlabel('x')
ax.set_ylabel('y')
# タイトル
plt.title('ランダムに2つのクラスに属するデータを生成')
# 凡例
ax.legend()
# プロットの表示
plt.show()
↓(出力)

この作成したデータにサポートベクターマシンを使います。
今回は独自関数を作り、その中にサポートベクターマシンの処理も入れています。
# 関数化(学習、決定協会、マージン、SVM)
def plot_boundar_margin_sv(X0, y0, X1, y1, kernel, C, xmin=-1, xmax=1, ymin=-1, ymax=1):
# サポートベクタマシンのインスタンス化
svc = SVC(kernel=kernel, C=C)
# 学習
svc.fit(np.vstack((X0, X1)), np.hstack((y0, y1)))
fig, ax = plt.subplots()
ax.scatter(X0[:, 0], X0[:, 1], marker='o', label='class 0′)
ax.scatter(X1[:, 0], X1[:, 1], marker='x', label='class 1′)
# 決定境界とマージンをプロットする
# np.meshgrid関数:各座標の要素列から格子座標を作成する、マス目の交点を出す
# np.linspace:第一引数以上、第二引数以下の、等間隔の配列を第三引数の要素数作成
xx, yy = np.meshgrid(np.linspace(xmin, xmax, 100), np.linspace(ymin, ymax, 100))
xy = np.vstack([xx.ravel(), yy.ravel()]).T
p = svc.decision_function(xy).reshape((100, 100))
# contour:等高線を描画, pは高さ
ax.contour(xx, yy, p, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['-', '-', '-', ])
# サポートベクタをプロット
ax.scatter(svc.support_vectors_[:, 0], svc.support_vectors_[:, 1], s=250, facecolors='none', edgecolors='black')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc='best')
plt.show()
関数を作りましたので、これを使ってプロットをしていきます。
# Cは、マージンの設定パラメータ
plot_boundar_margin_sv(X0, y0, X1, y1, kernel='linear', C=1e6)
↓(出力)
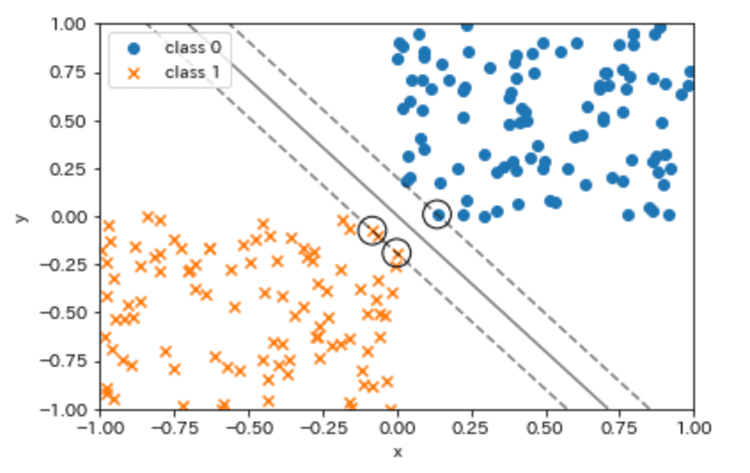
出力結果を見ると、2つのクラスに対して決定境界が引かれておりサポートベクタも算出されている事がわかります。
ちなみに、Cの値を調整することでマージンを変えて確認する事ができます。C=0.05でもう一度プロットしてみます。
plot_boundar_margin_sv(X0, y0, X1, y1, kernel='linear', C=0.05)
↓(出力結果)
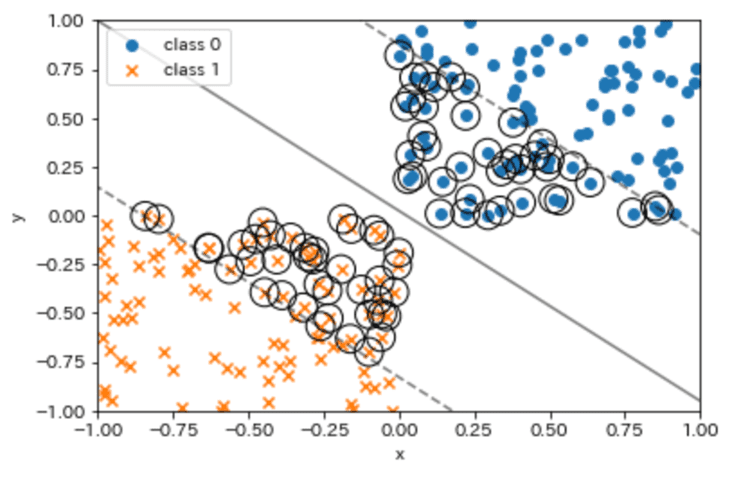
マージンが大きくなって、サポートベクタの個数も増えたことがわかります。このようにCの値を修正して試してみると理解が深まります。
さて、ここまでは直線の決定境界を見ていきましたが、必ずこの形で分類ができるとも限りませんので、直線以外のケースも見ていきます。
X = np.random.random(size=(100, 2))
# クラスを2つに分ける
y = (X[:, 1] > 2*(X[:, 0]-0.5)**2 + 0.5).astype(int)
fig, ax = plt.subplots()
ax.scatter(X[y == 0, 0], X[y == 0, 1], marker='x', label='class 0′)
ax.scatter(X[y == 1, 0], X[y == 1, 1], marker='o', label='class 1′)
ax.legend()
plt.show()
↓(出力結果)
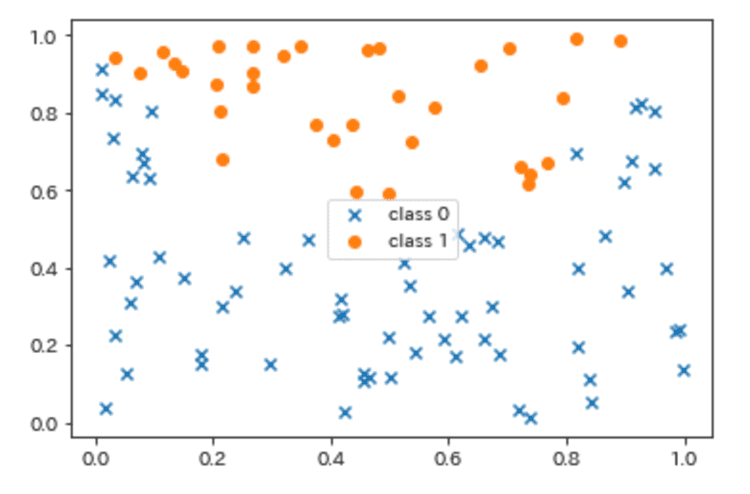
このように、一見すると直線では分類できなさそうなデータになりました。
それではこのデータを先程作った関数に当てはめてプロットしてみます。
X0, X1 = X[y == 0, :], X[y == 1, :]
y0, y1 = y[y == 0], y[y == 1]
# kernel='rbf':Radial Basis Function、動径基底関数(距離に基づいて値が決まる関数)を使用
plot_boundar_margin_sv(X0, y0, X1, y1, kernel='rbf', C=1e3, xmin=0, ymin=0)
↓(出力結果)
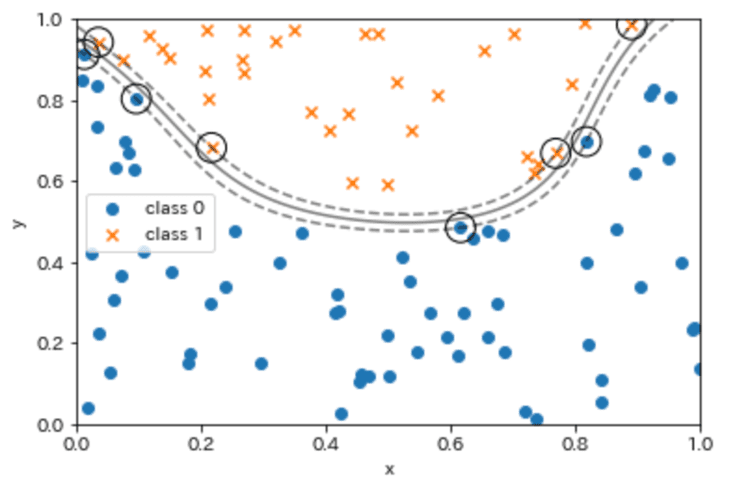
少し分かりづらいのでC=1にしたものがこちらです。
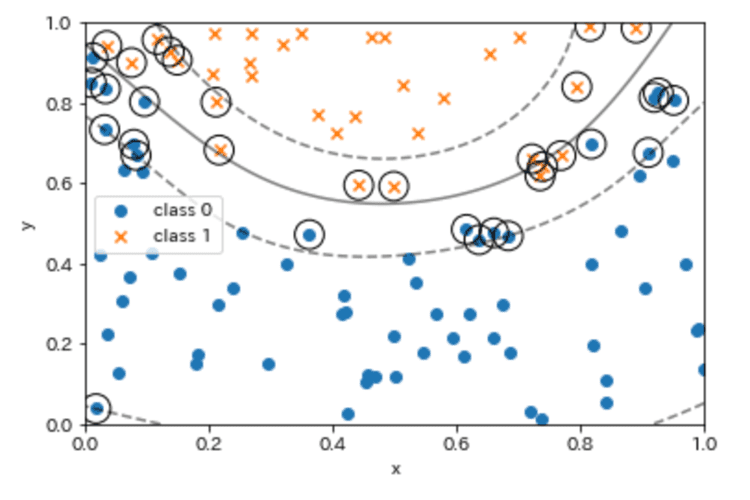
このように、scikit-learnのサポートベクターマシンを使った分類では様々なケースのデータを分析する事ができました。データが異なれば当然結果も異なりますので、できるようであれば皆様のお持ちのデータでも試してみることをおすすめします。
サポートベクターマシンを作って理解していく
今回は「サポートベクターマシン」という機械学習のアルゴリズムをPythonを使って構築していく流れを辿りました。データ自体はランダムで作ったデータを使いましたのですぐに自分ごととして捉えるのは難しいかもしれませんが、実際のデータが利用できる場合は実際のデータで是非チャレンジしてほしいです。
ただ、前処理をしっかりする必要があるため、めげずに色々試していきましょう。
インターネット・アカデミーは、Python講座が充実しています。Python認定スクールにもなっているため質の高い知識を得ることができ、基礎学習の先にあるそれぞれの目標を目指していくためには良い場所となります。ご興味ある方は各講座のページを覗いてみてください。
南波真之
デジタル人材育成・助成金のお役立ち資料をダウンロード

デジタル人材育成や助成金活用のお役立ち資料などをまとめてダウンロードしていただけます。コンサルタントへの無料相談をご希望の方はこちらからお問い合わせください。
- DX人材の育成&事例紹介 リスキリングのロードマップ付き
- デジタル人材育成に使える助成金制度
- デジタルスキル標準 役割別おすすめ講座

